Data Assimilation

There is a large number of observations of the magnetic field that constrain its evolution through time. Over thousand-year time scales, archaeomagnetic measurements from human artefacts and recent lava flows constrain the field through time. More recently, direct observations by humans constrain the field from the 16th century onwards. Since 1960 precise measurements by satellites give a global picture of field evolution, and continuously operating observatories have provided valuable data since the middle of the 19th century.
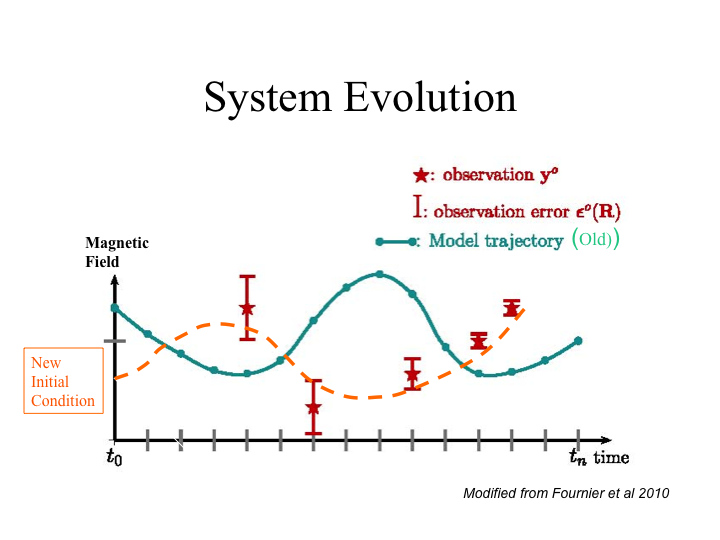
The evolution of the field is governed by a set of non-linear evolution equations (we can call them the dynamo equations in short). The idea of variational data assimilation is to use the dynamical equations in concert with observations to find the best model of field evolution through time. The evolution is governed by temperature variations in the core, and magnetic field strength, T and B respectively. The unknown in this set of equations is the initial condition of the variables (T and B). Figure 1 shows how the initial condition can affect the trajectory (field evolution) through time.

We have chosen a methodology called 4-D variational assimilation to find the best model of interior core conditions that leads to an evolution in time consistent with observation. The aim is to use the magnetostrophic equations in this exercise. At the moment we are using the magnetostrophic approximation together with a small amount of viscosity. Our aim is to ultimately remove this feature.
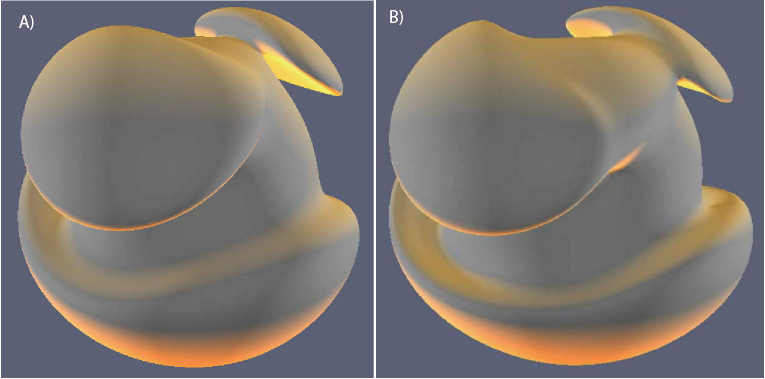
We have shown the methodology to be successful on a so-called toy problem, which has the driving force replaced by the Hall-effect. The aim of this exercise is to show the feasibility of the methodology. We perform closed-loop experiments in which we posit a known true initial condition, generate synthetic data at the surface of the Earth's core, and then use this data to try to recover the truth. In the circumstances reported in Li et al (2011) doi:10.1103/PhysRevE.84.056321 we find that we are able to recover the truth rather well when the data are exact. Figure 2 shows the result of this test in terms of an isosurface of the magnetic field.

Enlarged view: Figure 1: Shown schematically is the evolution of one component of the magnetic field through time, along with some observations. The data assimilation method (4DVar) aims to determine the initial condition for the magnetic field that leads to an evolution (trajectory) that agrees well with the observations. Shown is an initial guess for the magnetic field component that leads to an evolution in time given by the blue curve. It can be seen that the evolution is not in agreement with the observations. An improved initial condition (in orange) leads to a trajectory that is largely in agreement with the observations (and their associated error bars). Thus, our methodology systematically finds the best initial condition that leads to a dynamic evolution in agreement with observations. — Figure 1: Shown schematically is the evolution of one component of the magnetic field through time, along with some observations. The data assimilation method (4DVar) aims to determine the initial condition for the magnetic field that leads to an evolution (trajectory) that agrees well with the observations. Shown is an initial guess for the magnetic field component that leads to an evolution in time given by the blue curve. It can be seen that the evolution is not in agreement with the observations. An improved initial condition (in orange) leads to a trajectory that is largely in agreement with the observations (and their associated error bars). Thus, our methodology systematically finds the best initial condition that leads to a dynamic evolution in agreement with observations.

We have shown the methodology to be successful on a so-called toy problem, which has the driving force replaced by the Hall-effect. The aim of this exercise is to show the feasibility of the methodology. We perform closed-loop experiments in which we posit a known true initial condition, generate synthetic data at the surface of the Earth's core, and then use this data to try to recover the truth. In the circumstances reported in Li et al (2011) doi:10.1103/PhysRevE.84.056321 we find that we are able to recover the truth rather well when the data are exact. Figure 2 shows the result of this test in terms of an isosurface of the magnetic field.

Enlarged view: Figure 2: Shown is the |B|=1 isosurface for (a) the true initial state and (b) therecovered initial state from 2D observations taken at the surface of the spherical domain in which the inductive effects take place. The nonlinear evolution model was a so-called Hall-effect model, described in Li et al (2011). — Figure 2: Shown is the |B|=1 isosurface for (a) the true initial state and (b) therecovered initial state from 2D observations taken at the surface of the spherical domain in which the inductive effects take place. The nonlinear evolution model was a so-called Hall-effect model, described in Li et al (2011).

Our present work under MFECE is to tailor this scheme to the magnetostrophic equations, and to discover the limitations on the recovery of interior core properties that may exist.

Data Assimilation

Publications

Facilities